Prismatic pulse compressors for femtosecond, and ultrafast tunable lasers, were first introduced, via a single-prism configuration, in 1983 by Dietel et al. Multiple-prism pulse compressor arrays followed in 1984. Independently, the generalized multiple-prism dispersion theory applicable to prismatic pulse compression was introduced by Duarte and Piper in 1982 and then extended to second order derivatives in 1987. Interferometric Optics is pleased to offer prisms pairs manufacured with US made fused silica for the wavelengths of 620 nm and 800 nm. Specifications and prices are available in PDF form. Also, please visit our tutorial on prism pulse compression.

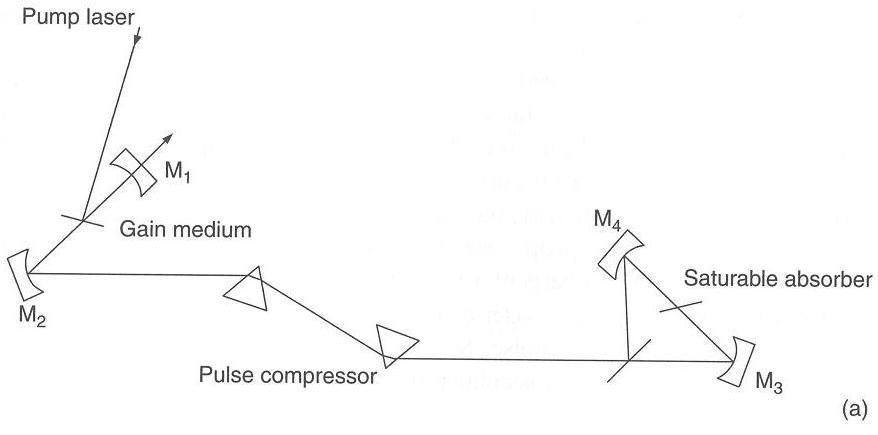
Note: the principles of prismatic pulse compression are described in F. J. Duarte, Tunable Laser Optics, 2nd Edition (CRC, New York, 2015) (see Chapter 4). This particular double-prism pulse compressor is depicted in a linear cavity as part of Fig. 1.17 which also includes a ring cavity configuration.

Bibliography

• W. Dietel et al., Intracavity pulse compression with glass: a new method of generating pulses shorter than 60 fs, Opt. Lett. 8, 4-6 (1983).
• F. J. Duarte and J. A. Piper, Dispersion theory of multiple-prism beam expander for pulsed dye lasers, Opt. Commun. 43, 303-307 (1982).
• R. L. Fork et al., Negative dispersion using pairs of prisms, Opt. Lett. 9, 150-152 (1984).
• F. J. Duarte, Generalized multiple-prism dispersion theory for pulse compression in ultrafast dye lasers, Opt. Quantum Electron. 19, 223-229 (1987).
• F. J. Duarte, Ray transfer matrix analysis of multiple-prism dye laser oscillators, Opt. Quantum Electron. 21, 47-54 (1989).
• F. J. Duarte, Prismatic pulse compression: beam deviations and geometrical perturbations, Opt. Quantum Electron. 22, 467-471 (1990).
• F. J. Duarte, Multiple-prism dispersion and 4 x 4 ray transfer matrices, Opt. Quantum Electron. 24, 49-53 (1992).
• L. Y. Pang, J. G. Fujimoto, and E. S. Kintzer, Ultrashort-pulse generation from high-power diode arrays by using intracavity optical nonlinearities, Opt. Lett. 17, 1599-1601 (1992).
• K. Osvay et al., Measurement of non-compensated angular dispersion and the subsequent temporal lengthening of femtosecond pulses in a CPA laser, Opt. Commun. 248, 201-209 (2005).
• F. J. Duarte, Equations for multiple-prism dispersion were derived earlier, Laser Focus World 42 (9), 11 (2006).
• L. Arissian and J-C. Diels, Carrier to envelope and dispersion control in a cavity with prism pairs, Phys. Rev. A. 75, 013814 (2007).
• F. J. Duarte (Ed.), Tunable Laser Applications, 3rd Ed. (CRC, New York, 2016) Chapter 13.
• F. J. Duarte, Generalized multiple-prism dispersion theory for laser pulse compression: higher order phase derivatives, Appl. Phys. B 96, 809-814 (2009).
• F. J. Duarte, Tunable organic dye lasers: physics and technology of high-performance liquid and solid-state narrow-linewidth oscillators, Progress in Quantum Electronics 36, 29-50 (2012).
• F. J. Duarte, Tunable laser optics: applications to optics and quantum optics, Progress in Quantum Electronics 37, 326-347 (2013).

Contact

Key words: pulse compresor, prism compression, prism compressor, prism compressors, prism pulse compression, prism pulse compressor, prism pulse compressors, multiple-prism compression, multiple-prism compressor, multiple-prism compressors, multiple-prism pulse compression, multiple-prism pulse compressor, multiple-prism pulse compressors.

Published on the 19th of November, 2006; updated on the 11th of January, 2024.