 Interferometric Optics Interferometric Optics
|
|---|
 Interferometric Optics Interferometric Optics
|
|---|
An additional application is the characterization of the emission transverse-mode structure in laser oscillators and/or laser resonators. In other words, the cavity and emission beam geometry can be optimized to achieve single-transverse-mode emission at maximum efficiency. This is a powerful design tool that saves time, resources, and effort in laser architecture and engineering.
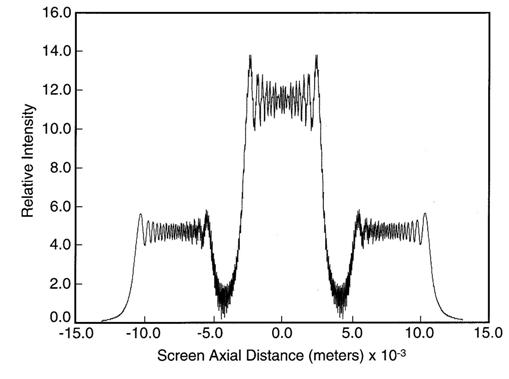
Keywords: N-slit interference, N-slit interferometer, N-slit interferometry, two-slit interference, two-slit interferometer, two-slit interferometry, double-slit interference, double-slit interferometer, double-slit interferometry, three-slit interference, three-slit interferometer, three-slit interferometry, triple-slit interference, triple-slit interferometer, triple-slit interferometry, four-slit interference, four-slit interferometer, four-slit interferometry
Published on the 15th of June, 2006; updated on the 31st of October, 2018.